Pythonista3で簡単なゲームをつくるために,ビリヤードのように平面上で円がぶつかる際の円の動きについて,高校時代のチャート式代数・幾何をひっぱりだしてきて考えてみた。奥付を見ると,昭和61年の改訂新版第2刷とあるが,まぁこんな基本的なことは30年やそこらでは変わらないであろう。
下の図のように,
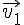
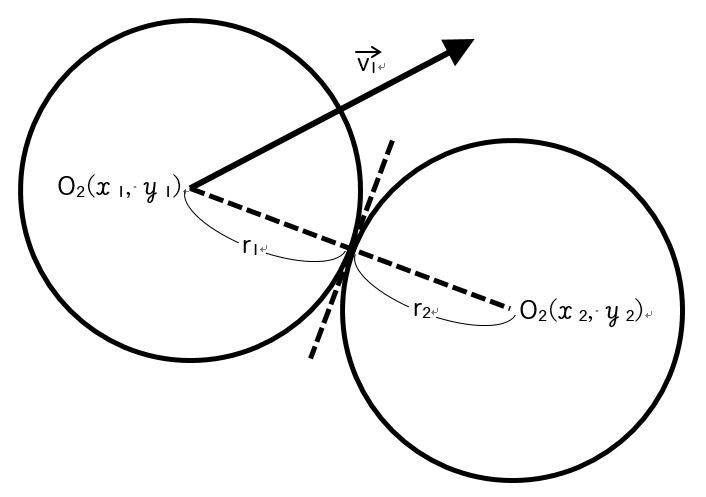
で移動する円O
1と静止している円O
2が衝突するとする。また,衝突した瞬間の円O
1の中心の座標は(x
1, y
1),円O
2の中心を座標を(x
2, y
2)とする。
「チャート式基本事項6ベクトルの表し方」より
任意のベクトルは,ただ一通りに,下の式の形で表される。
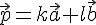 ( (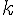 と と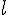 は実数) は実数) |
円の中心と中心を結んだ向きのベクトルを
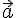
,
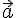
に垂直なベクトルを
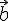
とすると,下の式で表すことができる。
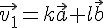
「チャート式基本事項10垂直条件」より
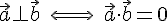
よって,) , ,) とすると, とすると,
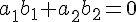
|
上の垂直条件は,
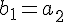
,
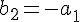
のときにも成り立つ。よって,下の図のように,以下の式が成り立つ。
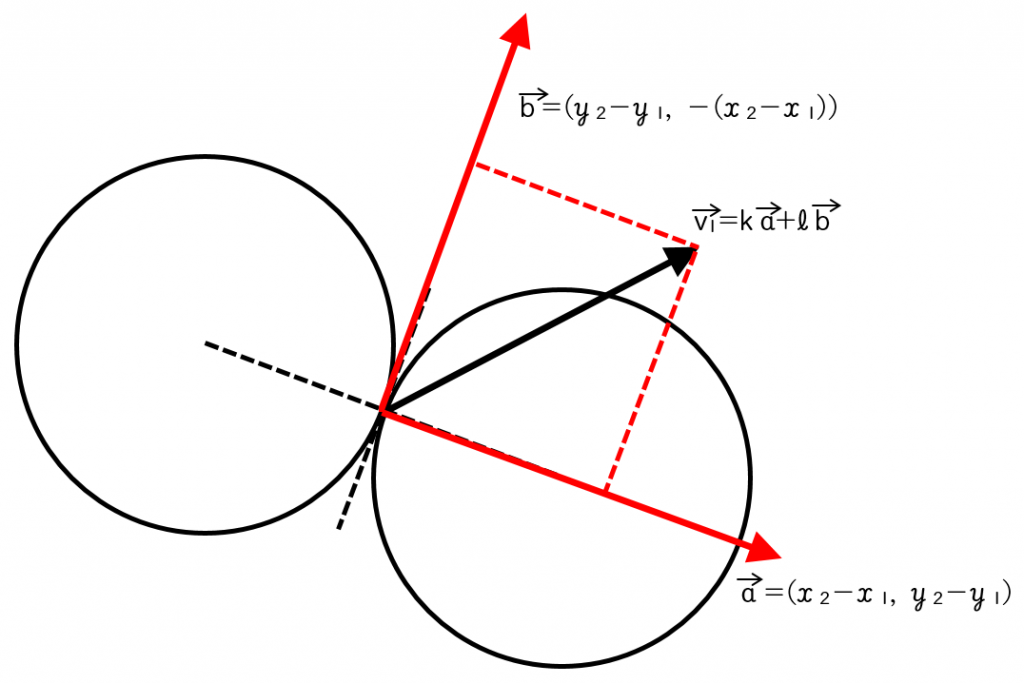
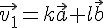
)
))
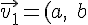)
とすると,以下の式が成り立つ。
%_26%_2B%_26l(y_%_7B2%_7D%_26-%_26y_%_7B1%_7D)%_5C%_5Cb%_26%_3D%_26k(y_%_7B2%_7D%_26-%_26y_%_7B1%_7D)%_26-%_26l(x_%_7B2%_7D%_26-%_26x_%_7B1%_7D)%_5Cend%_7Beqnarray%_7D)
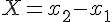
,
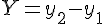
とすると,
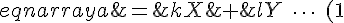%_5C%_5Cb%_26%_3D%_26kY%_26-%_26lX%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext(2)%_5Cend%_7Beqnarray%_7D)
これらを
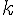
と
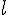
について解くと,下のようになる。
(1)の両辺にXをかけると,
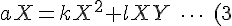)
(2)の両辺にYをかけると,
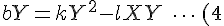%_7D)
(3)と(4)の両辺を足すと,
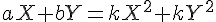
よって,
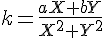
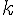
がもとめられれば,
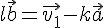
で
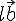
も簡単に求められるため,わざわざ
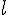
を求める必要はないが,一応続きを書いてみる。
同様に,(1)の両辺にYをかけると,
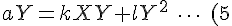)
(2)の両辺にXをかけると,
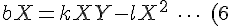)
(5)から(6)の両辺を引くと,
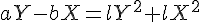
よって,
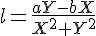
円がぶつかったときに,静止している円O
2に
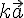
の速度ベクトルが加わり,移動している円O
1から
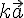
の速度ベクトルが失われる。
両方の円が移動している場合は,入れ替えて考え,速度ベクトルを合成する。