下の図のように,中心の座標が
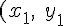)
で半径が
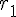
の円O
1と,中心の座標が
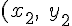)
で半径が
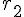
の円O
2があるとすると,この2つの当たり判定は,三平方の定理から,(1)のような式になります。
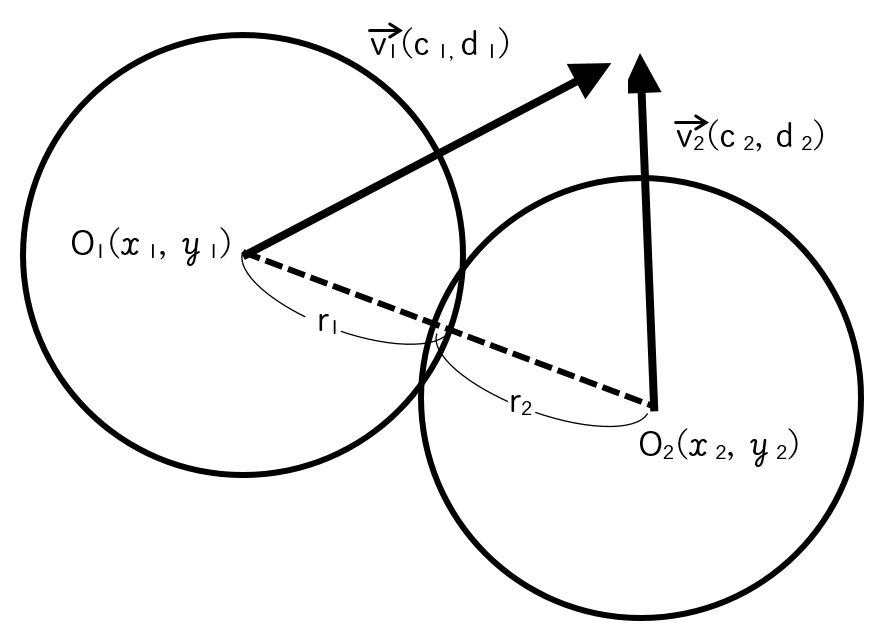
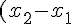%_5E2%_2B(y_%_7B2%_7D-y_%_7B1%_7D)%_5E2%_20%_20%_5Craisebox%_7B3%_7D%_7B%_5Crelstack%_7B%_3C%_7D%_7B%_3D%_7D%_7D%_20%_20(r_%_7B1%_7D%_2Br_%_7B2%_7D)%_5E2%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(1)%_7D)
①で右辺と左辺が等しい場合には問題ありませんが,多くの場合左辺が右辺よりも小さい状態で当たりが判定されます。これは2つの円が重なっている状態なので,衝突によって円の進む方向が変わっても,またすぐに当たりとして判定されてしまいます。そこで,2つの円が接した瞬間の円の中心の座標を計算で求めることにします。
「チャート式基本事項14直線のベクトル方程式」より
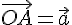 , ,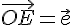 とすると, とすると,
点Aを通り, 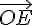 に平行な直線は,次のようなベクトル方程式で表される。 に平行な直線は,次のようなベクトル方程式で表される。
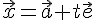 ( ( 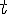 は実数) は実数)
| 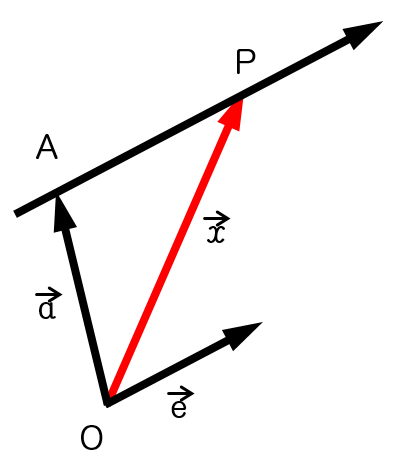 |
当たり判定時の原点から円の中心へのベクトルをそれぞれ
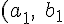)
,
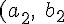)
とし,円の速度ベクトルをそれぞれ
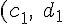)
,
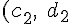)
,2つの円が接した瞬間の原点から円の中心へのベクトルをそれぞれ
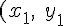)
,
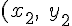)
とすると,下のようなベクトル方程式になる。
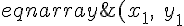%_26%_3D%_26(a_%_7B1%_7D%_2C%_5C%_3Bb_%_7B1%_7D)%_26%_2B%_26t%_26(c_%_7B1%_7D%_2C%_5C%_3Bd_%_7B1%_7D)%_26%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(2)%_7D%_5C%_5C%_26(x_%_7B2%_7D%_2C%_5C%_3By_%_7B2%_7D)%_26%_3D%_26(a_%_7B2%_7D%_2C%_5C%_3Bb_%_7B2%_7D)%_26%_2B%_26t%_26(c_%_7B2%_7D%_2C%_5C%_3Bd_%_7B2%_7D)%_26%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(3)%_7D%_5Cend%_7Beqnarray%_7D)
(
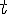
は実数)
(2)と(3)を展開すると,
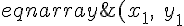%_26%_3D%_26(a_%_7B1%_7D%_26%_2B%_26c_%_7B1%_7Dt%_2C%_5C%_3Bb_%_7B1%_7D%_26%_2B%_26d_%_7B1%_7Dt)%_26%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(4)%_7D%_5C%_5C%_26(x_%_7B2%_7D%_2C%_5C%_3By_%_7B2%_7D)%_26%_3D%_26(a_%_7B2%_7D%_26%_2B%_26c_%_7B2%_7Dt%_2C%_5C%_3Bb_%_7B2%_7D%_26%_2B%_26d_%_7B2%_7Dt)%_26%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(5)%_7D%_5Cend%_7Beqnaray%_7D)
(4)と(5)を(1)に代入すると,
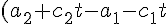%_5E2%_2B(b_%_7B2%_7D%_2Bd_%_7B2%_7Dt-b_%_7B1%_7D-d_%_7B1%_7Dt)%_5E2%_3D(r_%_7B1%_7D%_2Br_%_7B2%_7D)%_5E2%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(6)%_7D)
(6)で次のように置き換えると,
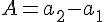
,
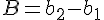
,
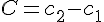
,
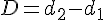
,
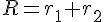
として代入すると,以下のようになる。
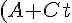%_5E2%_2B(B%_2BDt)%_5E2%_3DR%_5E2%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(7)%_7D)
これを展開して,
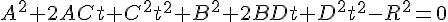
整理すると,次のような二次方程式になる。
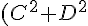t%_5E2%_2B2(AC%_2BBD)t%_2B(A%_5E2%_2BB%_5E2-R%_5E2)%_3D0%_5C%_3B%_5Ccdots%_5C%_3B%_5Ctext%_7B(8)%_7D)
(8)を二次方程式の解の公式
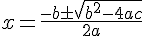
に当てはめると,
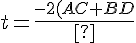%_5Cpm%_5Csqrt%_7B%_5Cleft%_7B2(AC%_2BBD)%_5Cright%_7D%_5E2-4(C%_5E2%_2BD%_5E2)(A%_5E2%_2BB%_5E2-R%_5E2)%_7D%_7D%_7B2(C%_5E2%_2BD%_5E2)%_7D)
円が接した時点(過去)の
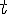
が知りたいので,2つの解の内,
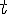
≦0の解をとる。